
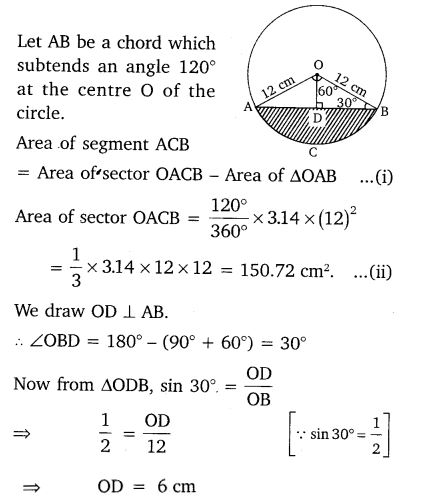
(Use π = 3.14 and √3 = 1.73)Īrea of the triangle formed by radii and chordĪrea of the minor segment = Area of the sector -Area of the triangle formed by radii and chordĪrea of the major segment = Area of the circle - Area of the minor segment Find the areas of the corresponding minor and major segments of the circle. A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. (iii) Area of the segment formed by the corresponding chord - area of the sector - area of the Δ formed between chord and radius of the circle (ii) Area of the sector with sector angle 60° (iii) area of the segment formed by the corresponding (ii) area of the sector formed by the arc In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. (ii) Area of the major segment = Area of the circle - Area of the minor segment (i) Area of the minor segment = (Area of the sector OAB) - (Area of ΔAOB formed with radius and chord)
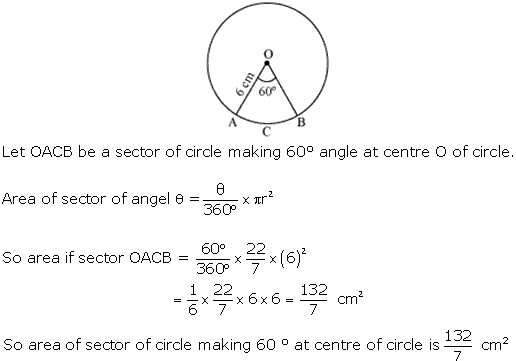
(Use π = 3.14)Īngle subtend by chord at centre = 90°. Find the area of the corresponding (i) minor segment (ii) major sector.

A chord of a circle of radius 10 cm subtends a right angle at the centre. Thus, the required area swept by the minute hand by 5 minutes = 154/3 cm 2. Now, area of the sector with r = 14 cm and θ = 30° ∴ Angle swept by the minute hand in 5 minutes = ∵ Angle swept by the minute hand in 60 minutes = 360° Find the area swept by the minute hand in 5 minutes. The length of the minute hand of a clock is 14 cm. Find the area of a quadrant of a circle whose circumference is 22 cm. Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60°.Īrea of the sector with r = 6 cm and θ = 60°


 0 kommentar(er)
0 kommentar(er)
